Teorema de Tales

Existen dos teoremas que reciben el nombre de Teorema de Tales, ambos obra del filósofo presocrático Tales de Mileto.

Primer teorema

Sean dos rectas (d) y (d') orientadas y concurrentes en un punto O. Sean A y A' dos puntos de (d), y B y B' dos puntos de (d'). Entonces:

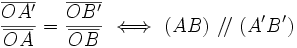
$frac {overline{OA'}} {overline{OA}} = frac {overline{OB'}} {overline{OB}} Longleftrightarrow (AB) /!/ (A'B')$

Es decir, que la igualdad de los cocientes equivale al paralelismo. Este teorema establece así una relación entre el álgebra y la geometría.

La primera figura corresponde a medidas algebraicas positivas - los vectores OA, OA', OB y OB' tienen la misma orientación que la rectas (d) y (d'), y la segunda a cocientes negativos.

Si se aplica el teorema, tenemos además otra consecuencia: si se orienta de la misma manera las dos rectas paralelas (AB) y (A'B'), es decir con el mismo vector, entonces el tercer cociente (de medidas algebraicas): A'B' / AB es igual a los dos anteriores.

A veces se reserva el nombre de teorema de Tales al sentido directo de la equivalencia, y el otro sentido recibe el nombre de recíproca del teorema de Tales.

Este teorema es un caso particular de los triángulos similares o semejantes.

interesante es para medir la altura de un árbol.

Medimos la longitud de su sombra a una hora determinada. = C
Medimos la longitud de la sombra de un objeto pequeño (por ejemplo un lápiz) en el mismo instante. = B
Medimos la longitud real del mismo cuerpo. = A

Y obtenemos $D = C left(frac{A}{B}right)$ donde D es la altura real del árbol.

También se puede relacionar para medir una distancia, cuya finidad no pueda ser medida, y apoyándose en un punto, se puede lograr.

Segundo teorema

Sea C un punto de la circunferencia de diámetro [AB], distinto de A y de B. Entonces el ángulo ACB es recto.

Este teorema es un caso particular de una propiedad de los puntos cocíclicos.

Prueba: OA = OB = OC = r, radio del círculo. Por lo tanto OAC y OBC son isósceles. La suma de los ángulos del triángulo ABC vale $2α + 2β = π$ (radianes). Dividiendo por dos, se obtiene $<!BCA!> = alpha + beta = frac {pi} 2$ (o 90º). Además dice que la bisectriz de un triángulo corta al lado opuesto del ángulo con la bisectriz en dos segmentos iguales

Hipotenusa (al cuadrado) = C(Al cuadrado) + C(Al cuadrado, es decir AB²=CA²+CB². En conclusión se forma un triangulo rectangulo.